"A casino offers a game of chance for a single player in which a fair coin is tossed at each stage. The pot starts at 2 dollars and is doubled every time a head appears. The first time a tail appears, the game ends and the player wins whatever is in the pot. Thus the player wins 2 dollars if a tail appears on the first toss, 4 dollars if a head appears on the first toss and a tail on the second, 8 dollars if a head appears on the first two tosses and a tail on the third, 16 dollars if a head appears on the first three tosses and a tail on the fourth, and so on. In short, the player wins 2k dollars, where k equals number of tosses. What would be a fair price to pay the casino for entering the game?
To answer this, we need to consider what would be the average payout: with probability 1/2, the player wins 2 dollars; with probability 1/4 the player wins 4 dollars; with probability 1/8 the player wins 8 dollars, and so on. The expected value is thus
Assuming the game can continue as long as the coin toss results in heads and in particular that the casino has unlimited resources, this sum grows without bound and so the expected win for repeated play is an infinite amount of money. Considering nothing but the expected value of the net change in one's monetary wealth, one should therefore play the game at any price if offered the opportunity. Yet, in published descriptions of the game, many people expressed disbelief in the result. Martin quotes Ian Hacking as saying "few of us would pay even $25 to enter such a game" and says most commentators would agree.[2] The paradox is the discrepancy between what people seem willing to pay to enter the game and the infinite expected value."
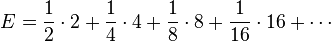
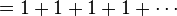
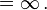
No comments:
Post a Comment